The last equation from Part 3, i.e. (A1.7) is soluble by standard methods to give the analytical solution:
Where:
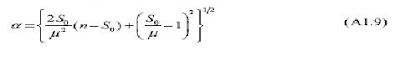And also:
When you graph (A1.8), you get a curve that looks something like this:
Comment on Hypothetical Graphical Illustration depicting the relationship between R (the removals) and t (time) inferred by equation (A1.8): When the crisis commences, the number of removals in the hedge fund sub-community grows exponentially as shown by the trajectory between point a and point b in the graph above. The removal rate then slows down somewhere after point b, and levels out between point b and point c. Between points c and d, the rate of removals gradually, albeit negligibly, slows down, until it falls steeply between points d and points e. At point e, there are no more removals and the crisis would have 'ended'. When deriving a numerical solution, using the Runge-Kutta-Fehlberg (R-K-F) algorithm, which is very efficient in that it only requires six evaluations per step, the errors are larger when the graph is at steepest descent, i.e, between points d and point e. Therefore, as dR/dt → -∞ , the accuracy of the model diminishes. The general rule is: 'the higher the infection rate the steeper the curve'. Furthermore, the higher the infection rate the shorter the time period required for the number of removals to level out. Clearly higher infection rates lead to higher values of R∞ (see equation (A1.12) for more details on R∞).
Therefore, the curve illustrating the rate of 'removals' in the hedge-fund industry with respect to time is given by the following equation, which in essence is the equation for computing the gradient of the Hypothetical Graphical Illustration depicting the relationship between R (the removals) and t (time) inferred by equation (A1.8) :
Computing the maximum casualty count is achieved by taking the limit of the contagion effect as t →∞ in equation (A1.8) which gives the equation for approximating the maximum casualty count as:
In the Hypothetical graphical illustration of equation (A1.8), the maximum casualty count is shown by the 'leveled-out' section of the trajectory between points b and c...Fitting the model into an existing Risk Management Framework
Risk management is more of an art than a science, and the best way to use this tool is to generate multiple random paths or random runs (Monte Carlo Simulation), starting at a hypothetical crisis 'commencement' date (to) and ending at another fixed date that is randomly selected, or 'picked' strategically. A real life 'infection-rate' β can be computed using real-life data, and other inputs for the model, like number of susceptible funds and the number of funds under stress at the specific time can be plugged-in from real-life data sources, or, hypothetical inputs can be generated if the risk manager choses to do that. To generate the random sample paths/random runs from the commencement date, the 'infection rate' and its components (e.g. leverage, correlation, e.t.c.) can be fudged around with, using a 'random' number generator. The multiple sample paths, are in essence, scenarios, that can be classed in from the worst case, to the best case scenarios, for detailed analysis. The most important thing to look-out for, are prevalent characteristics features of all sample paths - they will tell you what you need to know about your vulnerability to being wiped-out by the contagion effect.
Hopefully, you'll find this model as useful as I did.
-The End-
Please Note: This model is inspired by a paper co-authored by Jim Caldwell and Kei Shing Ng, titled: Deterministic Model in Contagious Disease, and is going through a continual overhaul to make it more robust. So far I've had this model critiqued by Rick Bookstaber, author of A Demon Of Our Own Design: Markets, Hedge Funds And The Perils of Financial Innovation, and he highlighted a lot of flaws, in the model and its presentation, that I'm currently addressing. Dr. Ernest Chan, the author of a quantitative text titled Quantitative Trading: How to Build Your Own Algorithmic Trading Business is also in the process of critiquing the model, and I'll also take his opinions on board. Furthermore, Dr. Jim Caldwell, the originator of the model I drew analogies from, also gave me a few pointers on how to make the model more realistic, and I'll also be taking his pointers on board. I also benefited from Eric Falkenstein's critique of the model, and I will be taking his suggestions on board as well. Please stay tuned!
